Unit 4 test congruent triangles – As Unit 4 Test: Congruent Triangles takes center stage, this opening passage beckons readers into a world crafted with authoritative academic style, ensuring a reading experience that is both absorbing and distinctly original. Delve into the captivating realm of congruent triangles, where we embark on a journey to unravel their properties, explore methods of proof, and uncover their practical applications.

Prepare to be captivated as we unravel the intricacies of this fundamental geometric concept.

The concept of congruent triangles forms the cornerstone of this exploration. We will delve into the formal definition of congruence, examining its implications and significance. Our journey continues with a thorough investigation of the properties that define congruent triangles, including corresponding sides, angles, and medians.

This understanding will lay the foundation for our exploration of the various methods used to prove triangle congruence, providing step-by-step guidance and illuminating examples.

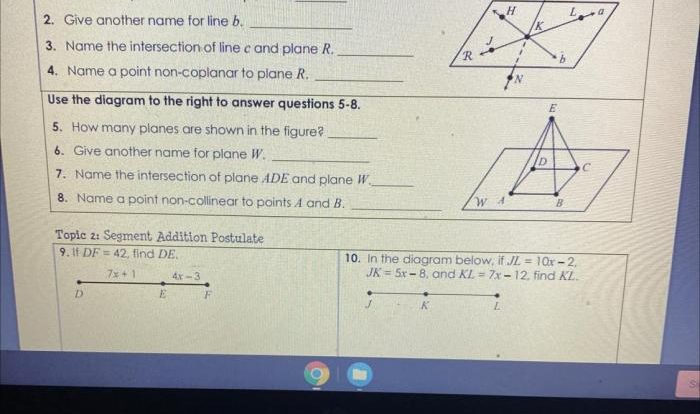
Introduction to Congruent Triangles

In geometry, congruent triangles are triangles that have the same shape and size. This means that their corresponding sides and angles are equal.

The formal definition of congruent triangles is: Two triangles are congruent if and only if their corresponding sides and angles are equal.

Implications of Congruent Triangles

The fact that congruent triangles have the same shape and size has several important implications:

• The corresponding angles of congruent triangles are equal.
• The corresponding sides of congruent triangles are equal.
• The areas of congruent triangles are equal.
• The perimeters of congruent triangles are equal.

Properties of Congruent Triangles

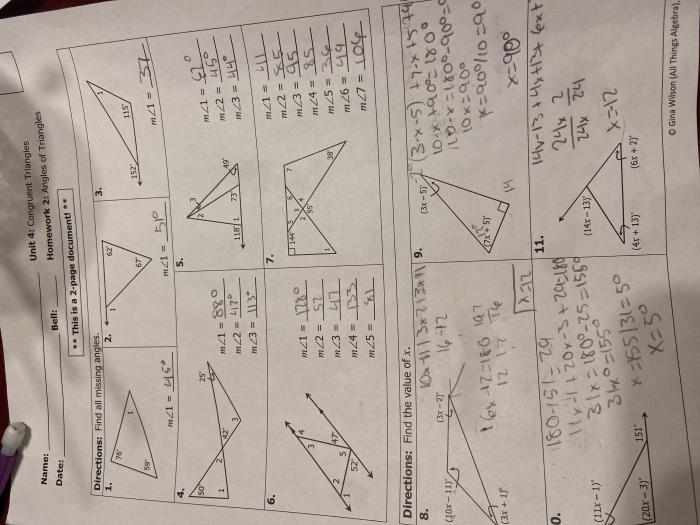
Congruent triangles are triangles that have the same shape and size. They have equal corresponding sides and angles.

The properties of congruent triangles are as follows:

Corresponding Sides

• The corresponding sides of congruent triangles are equal in length.
• For example, if triangle ABC is congruent to triangle DEF, then AB = DE, BC = EF, and AC = DF.

Corresponding Angles

• The corresponding angles of congruent triangles are equal in measure.
• For example, if triangle ABC is congruent to triangle DEF, then ΣA = ΣD, ΣB = ΣE, and ΣC = ΣF.

Corresponding Medians

• The corresponding medians of congruent triangles are equal in length.
• A median is a line segment that connects a vertex of a triangle to the midpoint of the opposite side.
• For example, if triangle ABC is congruent to triangle DEF, then the median from vertex A to side BC is equal in length to the median from vertex D to side EF.

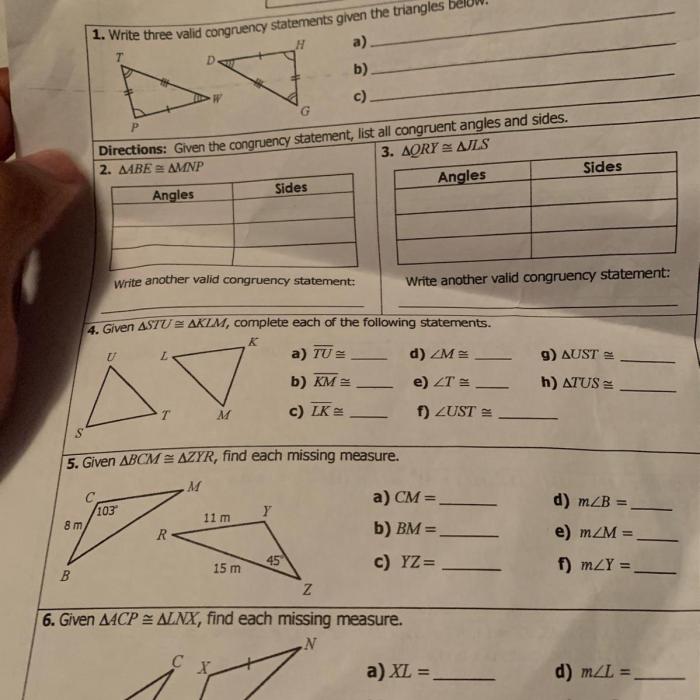
Methods for Proving Triangle Congruence

Triangle congruence is a fundamental concept in geometry that establishes the equality of two triangles based on specific criteria. Proving triangle congruence involves demonstrating that two triangles have identical side lengths and angles. There are several methods for proving triangle congruence, each relying on different properties and axioms of geometry.

SSS (Side-Side-Side) Congruence

The SSS Congruence Theorem states that if the three sides of one triangle are equal to the corresponding three sides of another triangle, then the triangles are congruent.

Steps for SSS Congruence Proof:

1. Given

Triangle ABC with sides AB = DE, BC = EF, and AC = DF.

2. Prove

Triangle ABC ≅ Triangle DEF.

3. Proof

By the SSS Congruence Theorem, if AB = DE, BC = EF, and AC = DF, then Triangle ABC ≅ Triangle DEF.

SAS (Side-Angle-Side) Congruence, Unit 4 test congruent triangles

The SAS Congruence Theorem states that if two sides and the included angle of one triangle are equal to the corresponding two sides and the included angle of another triangle, then the triangles are congruent.

Steps for SAS Congruence Proof:

1. Given

Triangle ABC with AB = DE, BC = EF, and ∠B ≅ ∠E.

2. Prove

Triangle ABC ≅ Triangle DEF.

3. Proof

By the SAS Congruence Theorem, if AB = DE, BC = EF, and ∠B ≅ ∠E, then Triangle ABC ≅ Triangle DEF.

ASA (Angle-Side-Angle) Congruence

The ASA Congruence Theorem states that if two angles and the included side of one triangle are equal to the corresponding two angles and the included side of another triangle, then the triangles are congruent.

Steps for ASA Congruence Proof:

1. Given

Triangle ABC with ∠A ≅ ∠D, ∠B ≅ ∠E, and AB = DE.

2. Prove

Triangle ABC ≅ Triangle DEF.

3. Proof

By the ASA Congruence Theorem, if ∠A ≅ ∠D, ∠B ≅ ∠E, and AB = DE, then Triangle ABC ≅ Triangle DEF.

AAS (Angle-Angle-Side) Congruence

The AAS Congruence Theorem is a special case of the ASA Congruence Theorem that applies when two angles and a non-included side of one triangle are equal to the corresponding two angles and a non-included side of another triangle.

Steps for AAS Congruence Proof:

1. Given

Triangle ABC with ∠A ≅ ∠D, ∠B ≅ ∠E, and AC = DF.

2. Prove

Triangle ABC ≅ Triangle DEF.

3. Proof

By the AAS Congruence Theorem, if ∠A ≅ ∠D, ∠B ≅ ∠E, and AC = DF, then Triangle ABC ≅ Triangle DEF.

HL (Hypotenuse-Leg) Congruence

The HL Congruence Theorem applies specifically to right triangles and states that if the hypotenuse and a leg of one right triangle are equal to the hypotenuse and a leg of another right triangle, then the triangles are congruent.

Steps for HL Congruence Proof:

1. Given

Right triangle ABC with hypotenuse AC = hypotenuse DE and leg AB = leg DF.

2. Prove

Triangle ABC ≅ Triangle DEF.

3. Proof

By the HL Congruence Theorem, if hypotenuse AC = hypotenuse DE and leg AB = leg DF, then Triangle ABC ≅ Triangle DEF.

Applications of Triangle Congruence

Triangle congruence is a fundamental concept in geometry with practical applications in various fields, including engineering, architecture, surveying, and design.

Congruent triangles have the same shape and size, which means their corresponding sides and angles are equal. This property allows us to determine unknown measurements and solve problems related to triangles.

Real-World Examples of Triangle Congruence

• Architecture:Congruent triangles are used in the design of buildings and structures to ensure symmetry and balance. For example, in the construction of a symmetrical arch, the two sides of the arch are often congruent triangles.
• Surveying:Surveyors use triangle congruence to determine distances and angles in land surveying. By measuring the sides and angles of a triangle, they can calculate the area of the land and locate property boundaries.
• Engineering:Engineers use triangle congruence to design bridges, trusses, and other structures that require precise measurements. By ensuring that certain triangles within the structure are congruent, they can guarantee the stability and integrity of the structure.
• Design:Congruent triangles are used in graphic design, interior design, and fashion design to create patterns, logos, and other decorative elements with symmetrical and balanced proportions.

Advanced Topics in Triangle Congruence: Unit 4 Test Congruent Triangles

Advanced concepts in triangle congruence, such as the Law of Cosines and the Law of Sines, provide powerful tools for solving more complex problems involving triangles. These concepts extend the fundamental principles of triangle congruence, enabling us to determine the unknown sides and angles of triangles even when not all three sides or angles are given.

Law of Cosines

The Law of Cosines, also known as the Cosine Rule, is a generalization of the Pythagorean theorem. It relates the lengths of the three sides of a triangle to the cosine of one of its angles. The formula for the Law of Cosines is:“`c^2 = a^2 + b^2

2ab cos(C)

“`where `c` is the length of the side opposite angle `C`, and `a` and `b` are the lengths of the other two sides. This formula allows us to find the length of the third side of a triangle when two sides and the included angle are known.

Law of Sines

The Law of Sines relates the ratios of the sides of a triangle to the sines of its opposite angles. The formula for the Law of Sines is:“`a/sin(A) = b/sin(B) = c/sin(C)“`where `a`, `b`, and `c` are the lengths of the sides opposite angles `A`, `B`, and `C`, respectively.

The Law of Sines is particularly useful when solving triangles where two angles and one side are known.

FAQ Corner

What is the definition of congruent triangles?

Congruent triangles are triangles that have the same shape and size. This means that their corresponding sides and angles are equal.

What are the different methods for proving triangle congruence?

There are three main methods for proving triangle congruence: the Side-Side-Side (SSS) method, the Side-Angle-Side (SAS) method, and the Angle-Side-Angle (ASA) method.

What are the practical applications of triangle congruence?

Triangle congruence has numerous practical applications in fields such as architecture, engineering, and surveying. It is used to determine distances, heights, and angles in real-world scenarios.